Context Free Grammar
Context Free
grammar or CGF, G is represented by four components that is G= (V, T,
P, S), where V is the set of variables, T the terminals, P the set of
productions and S the start symbol.
Example: The
grammar Gpal for palindromes is represented by
Gpal =
({P}, {0, 1}, A, P)
Where
A represents the set of five productions
1. P→∈
2. P→0
3. P→1
4. P→0P0
5. P→1P1
2. P→0
3. P→1
4. P→0P0
5. P→1P1
Derivation
using Grammar
Example 1: Leftmost Derivation
The inference that a * (a+b00) is in
the language of variable E can be reflected in a derivation of that
string, starting with the string E. Here is one such derivation:
E →E *
E → I * E →
a * E →a * (E) →
a * (E + E) → a * (I + E) →
a * (a + E) →a * (a + I) →
a * (a + I0) → a * (a + I00) →
a * (a + b00)
Leftmost Derivation - Tree
Example 2:
Rightmost Derivations
The derivation of
Example 1 was actually a leftmost derivation. Thus, we can describe
the same derivation by:
E→
E * E → E *(E) →
E * (E + E) →
E * (E + I) →
E * (E +I0) → E * (E + I00) →
E * (E + b00) →
E * (I + b00) →
E * (a +b00) → I * (a + b00) →
a * (a + b00)
We can also
summarize the leftmost derivation by saying
E → a * (a + b00), or express several steps of the derivation by expressions such as E * E → a * (E).
E → a * (a + b00), or express several steps of the derivation by expressions such as E * E → a * (E).
Rightmost
Derivation - Tree
There is a rightmost derivation that
uses the same replacements for each variable, although it makes the
replacements in different order. This rightmost derivation is:
E →
E * E → E * (E) →
E * (E + E) →
E * (E + I) →
E * (E + I0) → E * (E + I00) →
E * (E + b00) →
E * (I + b00)
→ E * (a + b00) →
I * (a + b00) → a * (a + b00)
This derivation
allows us to conclude E → a * (a +
b00)
Consider the
Grammar for string(a+b)*c
E→E
+ T | T
T→
T * F | F
F→
( E ) | a | b | c
Leftmost
Derivation
E→T→T*F→F*F→(E)*F→(E+T)*F→(T+T)*F→(F+T)*F
→(a+T)*F
→(a+F)*F
→(a+b)*F→(a+b)*c
Rightmost
derivation
E→T→T*F→T*c→F*c→(E)*c→(E+T)*c→(E+F)*c→(E+b)*c→(T+b)*c→(F+b)*c→(a+b)*c
Example 2:
Consider the
Grammar for string (a,a)
S->(L)|a
L->L,S|S
Leftmost derivation
S→(L)→(L,S)→(S,S)→(a,S)→(a,a)
Rightmost
Derivation
S→(L)→(L,S)→(L,a)→(S,a)→(a,a)
The Language
of a Grammar
If G(V,T,P,S) is a
CFG, the language of G, denoted by L(G), is the set of terminal
strings that have derivations from the start symbol.
L(G) = {w in T | S → w}
L(G) = {w in T | S → w}
Sentential
Forms
Derivations from the start symbol produce strings that have a special
role called “sentential forms”. That is if G = (V, T, P, S) is a
CFG, then any string in (V → T)*
such that S →a
is a sentential form. If S →a,
then is a left – sentential form, and if S →a
, then is a right – sentential form. Note that the language L(G)
is those sentential
forms that are in T*; that is they consist solely of terminals.
forms that are in T*; that is they consist solely of terminals.
For example, E * (I
+ E) is a sentential form, since there is a derivation
E →
E * E → E * (E) →
E * (E + E) → E * (I + E)
However this
derivation is neither leftmost nor rightmost, since at the last step,
the middle E is replaced.
As an example of a
left – sentential form, consider a * E, with the leftmost
derivation.
E →
E * E → I * E →
a * E
Additionally, the
derivation
E → E * E → E * (E) → E * (E + E)
E → E * E → E * (E) → E * (E + E)
Shows that
E * (E + E) is a right – sentential form.
E * (E + E) is a right – sentential form.
Ambiguity
A context – free
grammar G is said to be ambiguous if there exists some w ∈L(G)
which has at least two distinct derivation trees. Alternatively,
ambiguity implies the existence of two or more left most or
rightmost derivations.
Ex:-
Consider the
grammar G=(V,T,E,P) with V={E,I}, T={a,b,c,+,*,(,)}, and
productions.
E→I,
E→E+E,
E→E*E,
E→(E),
I→a|b|c
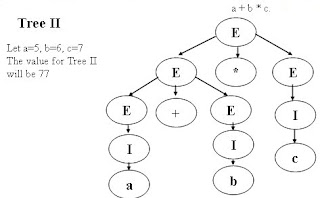
Consider two derivation trees for a + b
* c.
Now unambiguous
grammar for the above
Example:
E→T,
T→F,
F→I,
E→E+T,
T→T*F,
F→(E),
I→a|b|c
Inherent
Ambiguity
A CFL L is said to be inherently ambiguous if all its grammars are ambiguous
Example:Condider the Grammar for string aabbccdd
S→AB | C
A→ aAb | ab
B→cBd | cd
C→ aCd | aDd
D->bDc | bc
A CFL L is said to be inherently ambiguous if all its grammars are ambiguous
Example:Condider the Grammar for string aabbccdd
S→AB | C
A→ aAb | ab
B→cBd | cd
C→ aCd | aDd
D->bDc | bc
Parse tree for
string aabbccdd
Applications
of Context – Free Grammars
- Parsers
- The YACC Parser Generator
- Markup Languages
- XML and Document type definitions





No comments:
Post a Comment